what does it mean for two figures to be congruent

Relationship between ii figures of the same shape and size, or mirroring each other

An example of congruence. The two triangles on the left are congruent, while the tertiary is similar to them. The last triangle is neither congruent nor similar to whatever of the others. Congruence permits alteration of some properties, such as location and orientation, but leaves others unchanged, like distances and angles. The unchanged properties are called invariants.

In geometry, two figures or objects are congruent if they have the same shape and size, or if one has the aforementioned shape and size as the mirror image of the other.^[1]

More formally, two sets of points are called congruent if, and merely if, one tin can be transformed into the other past an isometry, i.e., a combination of rigid motions, namely a translation, a rotation, and a reflection. This means that either object can be repositioned and reflected (simply not resized) so as to coincide precisely with the other object. And so ii distinct plane figures on a piece of paper are coinciding if nosotros can cut them out and then match them upwardly completely. Turning the paper over is permitted.

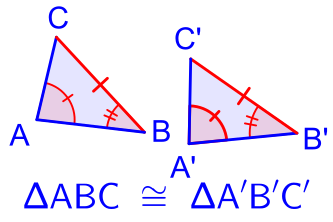
This diagram illustrates the geometric principle of bending-angle-side triangle congruence: given triangle ABC and triangle A'B'C', triangle ABC is congruent with triangle A'B'C' if and only if: angle CAB is congruent with angle C'A'B', and bending ABC is congruent with angle A'B'C', and BC is congruent with B'C'. Note hatch marks are used here to testify angle and side equalities.

In unproblematic geometry the word congruent is often used as follows.^[2] The word equal is oftentimes used in place of coinciding for these objects.

Two line segments are congruent if they take the same length.
Two angles are congruent if they have the same measure.
Two circles are congruent if they have the same bore.

In this sense, ii aeroplane figures are congruent implies that their respective characteristics are "congruent" or "equal" including non but their corresponding sides and angles, but also their corresponding diagonals, perimeters, and areas.

The related concept of similarity applies if the objects take the same shape but practice not necessarily accept the aforementioned size. (Well-nigh definitions consider congruence to be a class of similarity, although a minority require that the objects have different sizes in order to qualify as similar.)

Determining congruence of polygons

The orange and green quadrilaterals are congruent; the blue is not coinciding to them. All three take the same perimeter and area. (The ordering of the sides of the blue quadrilateral is "mixed" which results in two of the interior angles and 1 of the diagonals not being coinciding.)

For two polygons to be congruent, they must have an equal number of sides (and hence an equal number—the aforementioned number—of vertices). 2 polygons with n sides are congruent if and only if they each have numerically identical sequences (even if clockwise for i polygon and counterclockwise for the other) side-angle-side-angle-... for due north sides and due north angles.

Congruence of polygons can be established graphically as follows:

First, match and label the corresponding vertices of the ii figures.
2d, draw a vector from i of the vertices of the ane of the figures to the corresponding vertex of the other figure. Translate the first figure past this vector and so that these two vertices friction match.
Third, rotate the translated figure about the matched vertex until i pair of respective sides matches.
Fourth, reflect the rotated figure about this matched side until the figures match.

If at whatever fourth dimension the step cannot be completed, the polygons are non congruent.

Congruence of triangles

Two triangles are congruent if their corresponding sides are equal in length, and their corresponding angles are equal in measure.

If triangle ABC is congruent to triangle DEF, the relationship tin be written mathematically every bit:

\triangle \mathrm {ABC} \cong \triangle \mathrm {DEF} .

In many cases it is sufficient to found the equality of three corresponding parts and use 1 of the following results to deduce the congruence of the ii triangles.

The shape of a triangle is determined upwardly to congruence by specifying 2 sides and the angle between them (SAS), 2 angles and the side betwixt them (ASA) or two angles and a corresponding next side (AAS). Specifying two sides and an adjacent angle (SSA), however, tin yield two distinct possible triangles.

Determining congruence

Sufficient evidence for congruence between two triangles in Euclidean space tin be shown through the following comparisons:

SAS (side-bending-side): If two pairs of sides of 2 triangles are equal in length, and the included angles are equal in measurement, so the triangles are congruent.
SSS (side-side-side): If three pairs of sides of two triangles are equal in length, then the triangles are congruent.
ASA (angle-side-bending): If two pairs of angles of two triangles are equal in measurement, and the included sides are equal in length, and so the triangles are congruent.

The ASA postulate was contributed by Thales of Miletus (Greek). In virtually systems of axioms, the three criteria – SAS, SSS and ASA – are established as theorems. In the School Mathematics Study Group organisation SAS is taken equally one (#15) of 22 postulates.

AAS (angle-angle-side): If ii pairs of angles of two triangles are equal in measurement, and a pair of corresponding not-included sides are equal in length, and so the triangles are congruent. AAS is equivalent to an ASA condition, by the fact that if whatever two angles are given, so is the third angle, since their sum should be 180°. ASA and AAS are sometimes combined into a unmarried condition, AAcorrS – any two angles and a corresponding side.^[3]
RHS (right-angle-hypotenuse-side), as well known every bit HL (hypotenuse-leg): If ii right-angled triangles accept their hypotenuses equal in length, and a pair of shorter sides are equal in length, and then the triangles are congruent.

Side-side-angle

The SSA condition (side-side-angle) which specifies two sides and a non-included angle (besides known as ASS, or angle-side-side) does not by itself testify congruence. In gild to testify congruence, boosted information is required such as the measure of the corresponding angles and in some cases the lengths of the ii pairs of corresponding sides. At that place are a few possible cases:

If two triangles satisfy the SSA status and the length of the side opposite the angle is greater than or equal to the length of the adjacent side (SSA, or long side-short side-angle), then the two triangles are coinciding. The reverse side is sometimes longer when the respective angles are acute, but it is always longer when the respective angles are right or obtuse. Where the angle is a right angle, besides known as the hypotenuse-leg (HL) postulate or the right-angle-hypotenuse-side (RHS) condition, the tertiary side can be calculated using the Pythagorean theorem thus allowing the SSS postulate to be practical.

If two triangles satisfy the SSA condition and the corresponding angles are acute and the length of the side opposite the angle is equal to the length of the side by side side multiplied by the sine of the angle, then the two triangles are congruent.

If two triangles satisfy the SSA condition and the respective angles are astute and the length of the side opposite the angle is greater than the length of the adjacent side multiplied by the sine of the angle (merely less than the length of the side by side side), and then the two triangles cannot be shown to be congruent. This is the ambiguous instance and ii unlike triangles tin can exist formed from the given information, merely farther information distinguishing them tin lead to a proof of congruence.

Angle-angle-angle

In Euclidean geometry, AAA (angle-angle-angle) (or just AA, since in Euclidean geometry the angles of a triangle add together upwardly to 180°) does not provide information regarding the size of the two triangles and hence proves but similarity and not congruence in Euclidean space.

Nevertheless, in spherical geometry and hyperbolic geometry (where the sum of the angles of a triangle varies with size) AAA is sufficient for congruence on a given curvature of surface.^[4]

CPCTC

This acronym stands for Corresponding Parts of Congruent Triangles are Congruent, which is an abbreviated version of the definition of congruent triangles.^[5] ^[6]

In more than detail, information technology is a succinct style to say that if triangles $ABC$ and $DEF$ are congruent, that is,

\triangle ABC\cong \triangle DEF,

with corresponding pairs of angles at vertices $A$ and $D$ ; $B$ and $E$ ; and $C$ and $F$ , and with corresponding pairs of sides $AB$ and $DE$ ; $BC$ and $EF$ ; and $CA$ and $FD$ , and so the following statements are truthful:

{\overline {AB}}\cong {\overline {DE}}

{\overline {BC}}\cong {\overline {EF}}

{\overline {AC}}\cong {\overline {DF}}

\bending BAC\cong \angle EDF

\angle ABC\cong \angle DEF

\bending BCA\cong \bending EFD.

The statement is often used as a justification in elementary geometry proofs when a determination of the congruence of parts of 2 triangles is needed after the congruence of the triangles has been established. For example, if ii triangles have been shown to be coinciding by the SSS criteria and a statement that corresponding angles are coinciding is needed in a proof, so CPCTC may exist used every bit a justification of this argument.

A related theorem is CPCFC, in which "triangles" is replaced with "figures" so that the theorem applies to whatsoever pair of polygons or polyhedrons that are congruent.

Definition of congruence in analytic geometry

In a Euclidean system, congruence is key; it is the counterpart of equality for numbers. In analytic geometry, congruence may be divers intuitively thus: 2 mappings of figures onto one Cartesian coordinate system are congruent if and only if, for any two points in the first mapping, the Euclidean distance between them is equal to the Euclidean distance between the corresponding points in the 2d mapping.

A more than formal definition states that two subsets A and B of Euclidean space R ^north are chosen congruent if in that location exists an isometry f : R ⁿ → R ⁿ (an element of the Euclidean group E(due north)) with f(A) = B. Congruence is an equivalence relation.

Congruent conic sections

Two conic sections are congruent if their eccentricities and one other distinct parameter characterizing them are equal. Their eccentricities found their shapes, equality of which is sufficient to establish similarity, and the 2nd parameter then establishes size. Since two circles, parabolas, or rectangular hyperbolas always have the same eccentricity (specifically 0 in the case of circles, ane in the case of parabolas, and ${\sqrt {ii}}$ in the case of rectangular hyperbolas), two circles, parabolas, or rectangular hyperbolas need to have only ane other common parameter value, establishing their size, for them to be congruent.

Congruent polyhedra

For 2 polyhedra with the same combinatorial type (that is, the same number E of edges, the same number of faces, and the same number of sides on corresponding faces), there exists a set of Due east measurements that can establish whether or not the polyhedra are congruent.^[7] ^[viii] The number is tight, pregnant that less than E measurements are not plenty if the polyhedra are generic amid their combinatorial type. Merely less measurements can piece of work for special cases. For instance, cubes have 12 edges, simply 9 measurements are enough to decide if a polyhedron of that combinatorial type is congruent to a given regular cube.

Congruent triangles on a sphere

As with aeroplane triangles, on a sphere two triangles sharing the same sequence of angle-side-bending (ASA) are necessarily coinciding (that is, they accept three identical sides and 3 identical angles).^[9] This can be seen as follows: One tin situate one of the vertices with a given bending at the south pole and run the side with given length up the prime meridian. Knowing both angles at either cease of the segment of fixed length ensures that the other two sides emanate with a uniquely determined trajectory, and thus will meet each other at a uniquely determined point; thus ASA is valid.

The congruence theorems side-bending-side (SAS) and side-side-side (SSS) also hold on a sphere; in addition, if two spherical triangles have an identical angle-bending-bending (AAA) sequence, they are congruent (unlike for airplane triangles).^[ix]

The aeroplane-triangle congruence theorem angle-angle-side (AAS) does non concord for spherical triangles.^[x] Equally in airplane geometry, side-side-angle (SSA) does not imply congruence.

Note

A symbol usually used for congruence is an equals symbol with a tilde above it, ≅, respective to the Unicode graphic symbol 'approximately equal to' (U+2245). In the Britain, the 3-bar equal sign ≡ (U+2261) is sometimes used.

Run into also

Euclidean plane isometry
Isometry

References

^ Clapham, C.; Nicholson, J. (2009). "Oxford Concise Dictionary of Mathematics, Congruent Figures" (PDF). Addison-Wesley. p. 167. Archived from the original on 29 October 2013. Retrieved two June 2017. {{cite web}}: CS1 maint: bot: original URL status unknown (link)
^ "Congruence". Math Open Reference. 2009. Retrieved 2 June 2017.
^ Parr, H. East. (1970). Revision Course in Schoolhouse mathematics. Mathematics Textbooks Second Edition. G Bell and Sons Ltd. ISBN0-7135-1717-4.
^ Cornel, Antonio (2002). Geometry for Secondary Schools. Mathematics Textbooks 2d Edition. Bookmark Inc. ISBN971-569-441-one.
^ Jacobs, Harold R. (1974), Geometry, Due west.H. Freeman, p. 160, ISBN0-7167-0456-0 Jacobs uses a slight variation of the phrase
^ "Congruent Triangles". Cliff'south Notes. Retrieved 2014-02-04 .
^ Borisov, Alexander; Dickinson, Mark; Hastings, Stuart (March 2010). "A Congruence Trouble for Polyhedra". American Mathematical Monthly. 117 (3): 232–249. arXiv:0811.4197. doi:10.4169/000298910X480081. S2CID 8166476.
^ Creech, Alexa. "A Congruence Problem" (PDF). Archived from the original (PDF) on November 11, 2013.
^ ^a ^b Bolin, Michael (September 9, 2003). "Exploration of Spherical Geometry" (PDF). pp. 6–7.
^ Hollyer, L. "Slide 89 of 112".

External links

Wikimedia Eatables has media related to Congruence.

The SSS at Cut-the-Knot
The SSA at Cut-the-Knot
Interactive animations demonstrating Congruent polygons, Coinciding angles, Congruent line segments, Coinciding triangles at Math Open Reference

lyleshawat.blogspot.com

Source: https://en.wikipedia.org/wiki/Congruence_%28geometry%29